Projektbeschreibung

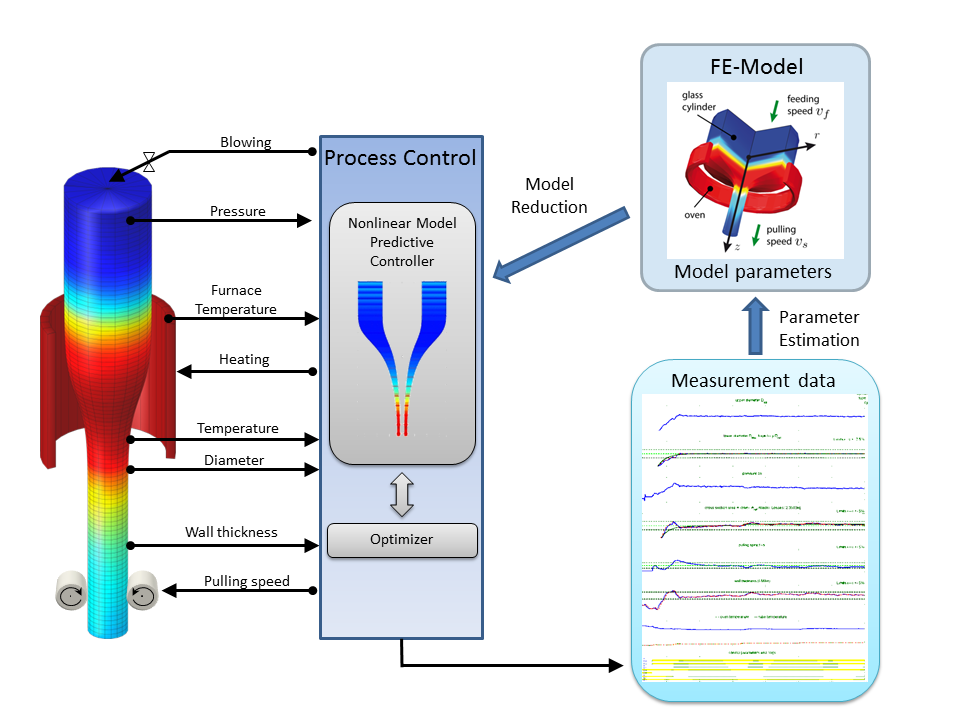
Die Optimierung der Prozessführung von verfahrenstechnischen Prozessen erfolgt meist anhand realitätsnaher Prozessmodelle. Charakteristisch für solche Prozesse sind hierbei auftretende starke Nichtlinearitäten. Ursächlich dafür sind die Physik des Prozesses (z.B. Strahlungsaustausch) sowie eventuelle nichtlineare Materialeigenschaften. Es ist deshalb von entscheidender Bedeutung, die räumlich verteilte Struktur der Prozesse nicht zu vernachlässigen.
Bei der Modellierung solcher Prozesse müssen mindestens die folgenden Aspekte betrachtet werden. Zum einen ist die numerische Berechnung (z.B. mittels Finite Elemente Methode) des raum-zeitlichen Verhaltens der Prozesse wegen der hohen Systemordnung der Modelle aufwändig. Aus diesem Grund eignet sich ein solches Modell nicht zur modellprädiktiven Regelung.  Die Qualität des Modells lässt sich jedoch verbessern, indem die Parameter der Prozesse durch historische Prozessdaten geschätzt und ergänzt werden. Die Parameterschätzung mit Hilfe von historischen Prozessdaten ist ein statistisches inverses Problem, dessen Lösung auch einen erheblichen Berechnungsaufwand erfordert.
Um diesen Berechnungsaufwand zu senken, werden Methoden zur Modellreduktion von räumlich verteilten, nichtlinearen Systemen benötigt. Die Modellreduktion von hochdimensionalen linearen Systemen ist Stand der Wissenschaft. Die Erforschung und Entwicklung von Verfahren zur nichtlinearen Modellreduktion befindet sich allerdings noch in der Anfangsphase und muss weiter ausgebaut werden. An dieser Stelle knüpft das vorliegende Projekt an und versucht, einen wesentlichen Beitrag zur Erschließung neuer Methoden und deren Umsetzung in die industrielle Anwendung zu leisten.